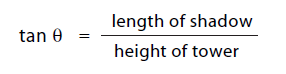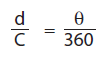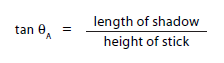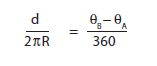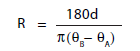TEACHER’S GUIDE:  ( download  http://www.stick.com.ar/guide.pdf )

 
Overview

This activity enables students to measure the circumference of Earth. Groups of students at two distant schools will take data and then collaborate, in essentially the same way that Eratosthenes measured Earth’s circumference millennia ago in Egypt.

 
Objectives

• Describe the geometry of how sunlight strikes Earth at different latitudes

• Describe how the circumference of Earth was first measured millennia ago

• Describe how to determine local noon

• Measure the angle of the sun at local noon

• Collaborate with another school some distance away to determine the circumference of Earth.

 Logistics

Your class will need measurements of the shortest shadow length and stick length to be taken at some other school located a considerable distance away, either north or south.

You will enter your school's information on the Stick Project website, <http://stick.com.ar/planilla.html/>, at the same time as the other school's information. Once the partner schools have shared the measurements, the circumference of the earth is automatically calculated.
 
National Standards Addressed

This activity addresses the following Benchmarks and National Science Education Standards (NSES):
 
Benchmarks, K-12: The Mathematical World

Symbolic Relationships

When a relationship is represented in symbols, numbers can be substituted for all but one of the symbols and the possible values of the remaining symbol computed. . . .

Shapes

Distances and angles that are inconvenient to measure directly can be found from measurable distances and angles using scale drawings or formulas.

Models

The basic idea of mathematical modeling is to find a mathematical relationship that behaves in the same way as the objects or processes under investigation. A mathematical model may give insight about how something really works or may fit observations very well without any intuitive meaning.
 
Benchmarks, K-12: The Nature of Science

The Scientific Enterprise
The early Egyptian, Greek, Chinese, Hindu, and Arabic cultures are responsible for many scientific and mathematical ideas and technological inventions.
 
NSES, K-12: History and Nature of Science

Science as a Human Endeavor
Individuals and teams have contributed and will continue to contribute to the scientific enterprise.

Historical Perspectives
In history, diverse cultures have contributed scientific knowledge and technologic inventions.
 
NSES, K-12: Unifying Concepts and Processes

Developing Student Understanding
• Evidence, models, and explanation
• Constancy, change, and measurement
 

NSES, K-12: Science as Inquiry

Abilities necessary to do scientific inquiry
• Design and conduct scientific investigations
• Use technology and mathematics to improve investigations and communications
• Formulate and revise scientific explanations and models using logic and evidence
 

Materials

For each student
      • A copy of the Student Activity Guide
 
For each group
• stick or dowel, about 60 centimeters (cm) long
• stiff cardboard (to provide a smooth, flat surface)
• measuring tape
• pieces of blank paper
• pencil
 
To be shared by several groups
• carpenter’s level
• mason's plumb line
 

STUDENT’S GUIDE:

THE ERATOSTHENES PROJECT
In this activity, you will work together with students at another school to measure the circumference of Earth. You will use the same methods and principles that Eratosthenes used more than two thousand years ago.

 
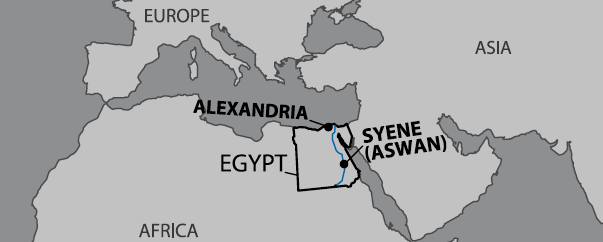
Eratosthenes was a Greek living in Alexandria, Egypt, in the third century, BC. He knew that on a certain day at noon in Syene, a town a considerable distance to the south, the sun shone straight down a deep well. This observation meant that the sun was then directly overhead in Syene, as shown in Figure 1.

 
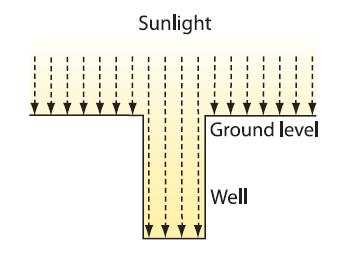
Figure 1:
Light rays shining straight down a well in Syene at noon, when the sun is directly overhead. No shadow is cast.

Eratosthenes also knew that when the sun was directly overhead in Syene, it was not directly overhead in Alexandria, as shown in Figure 2. Notice that in both drawings, the sun’s rays are shown as parallel.

 

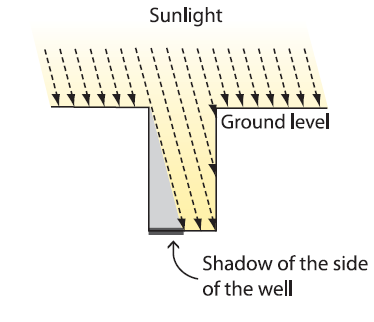
Figure 2:
Sunlight shining down a well in Alexandria at noon, on the same day as the observation shown in Figure 1. The sun is not directly overhead. The gray bar at the bottom left shows the shadow cast by the side of the well. The angle of the sun’s rays and the size of the shadow are exaggerated.

In Figure 2, the side of the well casts a shadow on the bottom.

Eratosthenes used a shadow like this to find the circumference of Earth. When the sun was directly overhead in Syene, he measured the shadow of an object in Alexandria at noon. From the length of the shadow, the height of the object, and the distance between Syene and Alexandria, he calculated the circumference of Earth. His value agreed quite well with the modern one.

 
How Eratosthenes Found the Circumference of Earth


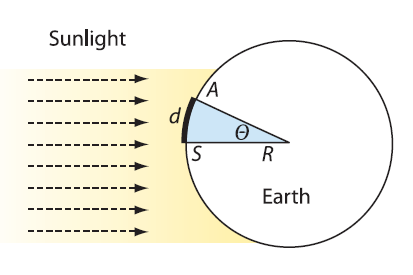
Figure 3:
The sun is directly overhead at noon at Syene (S). Alexandria is at point “A.”

How did he do it, more than two thousand years ago? Take a look at Figure 3. Syene is represented by point “S,” and Alexandria by point “A”. In Figure 3, the arc length between S and A is d, and the angle corresponding to the arc SA is ?. The radius of Earth is R. As suggested above, let’s assume that the sun’s rays are parallel. Since the ray that strikes Syene, at point S, is perpendicular to the surface of Earth, the sun is directly overhead there.When the sun was directly overhead in Syene, Eratosthenes measured the shadow of a tower in Alexandria at noon,1 shown in Figure 4. Since both the tower at A, which is perpendicular to Earth’s surface, and the ray of sunlight at point S both point to the center of Earth, and the rays of sunlight are parallel, the angle between the sunlight and the tower is equal to ? (Alternate interior angles are equal.)

 

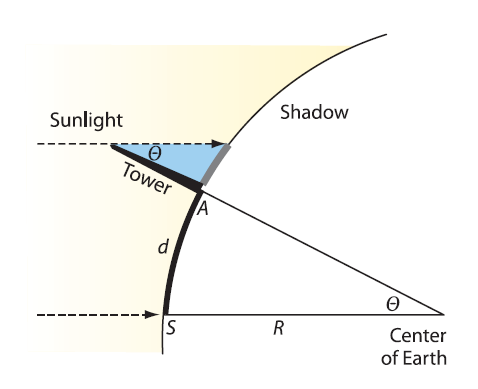
Figure 4:
The geometry of Eratosthenes’ measurement. He measured the length of the tower and its shadow at noon at Alexandria. Then he determined the angle of sunlight with the vertical, which is the same as the angle subtended by Syene (S) and Alexandria
(A) at the center of Earth.

 
The tower and its shadow form two sides of a right triangle, as shown in Figure 4. Although trigonometry hadn’t yet been invented, Eratosthenes’ procedure can be expressed in the language of trig as follows: The length of the shadow, the height of the tower (which he knew), and the angle ?, given here in degrees, are related by

 
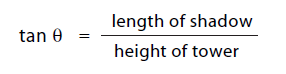
Inverting tan? gives the value of ?. Using ratio and proportion, the arc length d is the same fraction of Earth’s circumference C as ? is of 360 degrees.

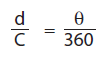
Rearranging for the circumference C,

How You Can Find the Radius of Earth
Rather than find Earth’s circumference, we suggest you find its radius, so that you can more easily compare your measured value with the accepted value.
Eratosthenes was lucky, because he knew of a place where the sun was directly overhead at noon on a certain day. Can you do the experiment even without that information?
Fortunately you can, as shown in Figures 5 and 6. You will make the shadow measurements at your school and share results with a class from a school at another location.
You can then do a subtraction to find the angle you need. Be sure to plan ahead—ideally, both  schools make the measurement on the same day.

 
 
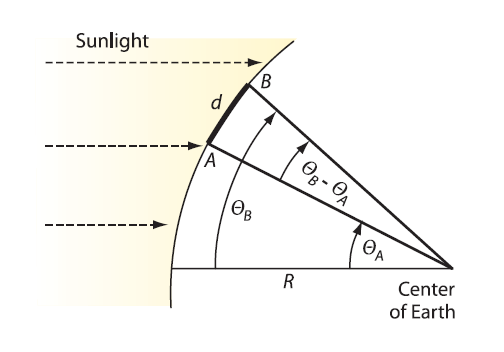
Figure 5:
The geometry for measuring the radius of Earth using the data of two collaborating schools separated by a north-south distance. Each will measure the angle of the sun, ?_A at one location and ?_B at the other, at local noon.
 
We need two points, A and B, separated by a north-south distance d, shown on Figure 5. The experiment will work best if d is as large as possible.Take a look at Figure 6. Your school and the collaborating school are represented by the points A and B, and the angles ?_A and ?_B correspond to points A and B.

 

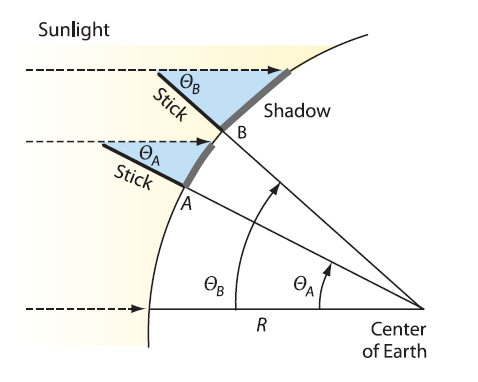
Figure 6:
The relationship among the direction of sunlight, the sticks, and
the two angles ?_A and ?_B.

At point A,

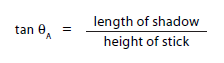
and likewise at point B.
Figures 5 and 6 show that the angle corresponding to the arc AB is just the difference  ?_B - ?_A We can find the radius of Earth in the same way that Eratosthenes found the circumference in equation.

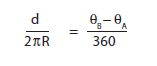
Rearranging and simplifying,



 
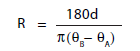
Making the Measurement at Local Noon

On any day, local noon is the instant when the sun reaches its highest point in the sky. To determine it, plant the stick in the ground, making sure the stick is vertical using a plumb bob or a carpenter’s level. In the late morning, measure the shadow’s length at regular time intervals. The shadow will get shorter as noon approaches, and then get longer again once noon has passed. The shortest length is what you will substitute into equation above to find the value of ?_B or ?_A for your location.
 
Below are three additional activities:
• How Shadows Change During the Day
• Shadows on Earth
• Latitude
 
How Shadows Change During the Day

If your students have not thought much about shadows,they might benefit by starting with this preliminary activity.Give each group a 5cm straw piece, a sheet of 21cm x 29cm paper, and some tape. Ask them to tape the straw so it stands in the center of the paper, as shown in Figure 7, and also to indicate the direction of north on one of the long sides. If you provide them with a compass, they can orient the paper.

 

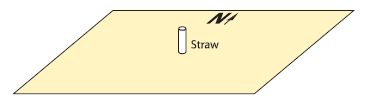
Figure 7:
Five-centimeter straw mounted vertically on a piece of paper.
Students predict and then measure the shadow of this straw at different times.

Their challenge is to imagine that this paper is set on level ground in sunlight and to predict the location and length of the shadow of the stick on the hour during the day. Discuss these predictions to bring out their thinking. Then have them do the experiment and compare their predictions and results.

  
Shadows on Earth

Materials for each group: five 4-cm straw pieces, tape, and a piece of 21cm x 29cm paper.

Explain to students that they will make a model of shadows at different points on Earth. Have them draw a straight line across a piece of 21cm x 29cm paper and tape the five straw pieces, equally spaced, along this line, so the straws stand straight up. Ask how the paper and straws could be a model of sticks placed at different locations on Earth (curve the paper, with the straws on the convex side).

Explain that to avoid damaging their eyes, they should never look directly at the sun. In sunlight, ask students how the paper and straws can model the Eratosthenes experiment. (Facing the sun, hold the paper at the ends of the long sides and curve it so the straws point out. Turn the paper to make the shadow of one straw disappear. Make this straw point directly at the sun. The straw without a shadow models the well at Syene.) Have students describe what happens to the shadows of the other straws and relate the shadow of each one to its position. Ask students to relate these shadows to the shadows Eratosthenes used to measure Earth’s circumference. See Figure 8.

Figure 8:
Model of shadows of sticks at noon, at different
latitudes and the same longitude.

Extension Activity: Latitude

Once experimentation is complete and the results reported, you can have students relate the measurements they have made to the definition of latitude.
a. Ask them to define latitude (the length of arc, or angle from the center of Earth, measured north or south from the equator).
b. Referring them to Figure 3, ask them to assume that point S is on the equator. Ask on what day the sun would be directly overhead at noon at S.
c. If your students made their shadow measurement on the vernal or autumnal equinox, the resulting angle would be equal to the latitude, as shown in Figure 3 (remember point S is on the equator). If possible, have them try to do this by measuring the shadow of a stick on or near March 21 or September 21.
d. In the Eratosthenes experiment, the angle (?_B - ?_A) is the same as the difference in latitude of the two schools, so students could determine this difference immediately by subtracting the two latitudes of the collaborating schools. Of course, we want students to make measurements and compare, rather than look up the answer in an atlas. If students point this out, you can remind them that they are reenacting an historical experiment.

 
ADDITIONAL ACTIVITIES
 
Notes on Introduction

In the discussion of Figures 1 and 2, which show sunlight in wells at two different locations, we assume the following:
• The rays of sunlight are parallel (see next section for more detail)
• The sides of the well are vertical.
 

Notes on How Eratosthenes Found the Circumference of Earth

Here are Eratosthenes’ assumptions:
Earth is a sphere. In fact, Earth bulges by about .3% at the equator, but we can safely neglect this difference.
The sun is very far away, so sunlight can be represented by parallel rays. The sun is indeed very far away, but it is not a point source, since its diameter is about 1/100 of the Earth sun distance.



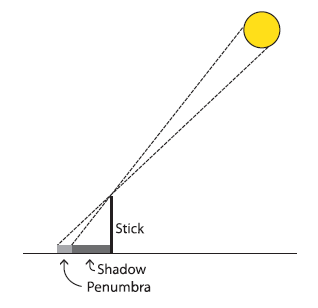
Figure 9:
Notice the penumbra—the partially illuminated region—at the
end of the stick’s shadow (drawing not to scale).
 
As shown in Figure 9, there is a penumbral region at the end of the shadow, a region only partially illuminated by the sun. If the stick is 1 meter (m) long, the penumbral region will be more than 1 centimeter (cm) wide, which limits the accuracy of the measurement of the shadow length. The penumbra size scales up with the length of the stick, so using a longer stick does not increase the accuracy of the measurement.

Alexandria is directly north of Syene: This is only approximately true. Find an atlas and compare the location of Alexandria and Aswan (built on the site of Syene).

You might ask students to comment on Eratosthenes’ assumptions, considering that he was working more tan 2,000 years ago.

 
Notes on How You Can Find the Radius of Earth

Ask students to discuss the distance d between the two schools. Is it better for d to be large or small? (large) Why? (The larger d, the larger the value of the angle ?_B - ?_A The larger this angle, the smaller the percentage error in its measurement). Find the location of the two schools and ask students how to find the distance between them (use the scale on the map). Ask how well the two schools line up north-tosouth.

Discuss how an east-west displacement might affect the outcome of the experiment. (Convert the difference in longitudes of the two schools into a time difference, using ratio and proportion and the fact that 360° of longitude corresponds to 24 hours. Then compare the difference with the uncertainty in identifying local noon.)

Note that near local noon, the shadow length does not change much with time. For this reason, missing local noon by a few minutes is not important. Suggest that students practice measuring the shadow length at noon in advance. If you need to look up the time of local noon, see the last reference.

Ask students how to select a suitable date for both schools to make measurements. Should they check the weather forecast first?

Try making the measurement of the shadow length yourself. If possible, drive the stick into the ground, and check with the level, or a plumb line, to be sure that the stick is vertical.

Tape copy paper on top of the sheet of cardboard, and check with the level to make sure that this surface is horizontal. Be sure your stick is short enough so the shadow doesn’t extend off the paper. Ask students to describe what height they will measure (the distance from the top of the stick to the surface where they see the shadow).

NOTES ON THE ACTIVITIES
 
References
 
The experience is summarized in the following video. In this video the subtitles in English can be activated.
https://www.youtube.com/watch?v=4VVx0RTLCEA&feature=emb_logo
 
Find out the latitude of my city
https://www.latlong.net/
 
Solar noon in my city

https://www.timeanddate.com/sun/argentina/san-juan

 https://sunsetsunrisetime.com/sun
 
https://salidaypuestadelsol.com/sun
 
 
What Is Solar Noon?

https://www.timeanddate.com/astronomy/solar-noon.html

 
One of the things we do is "measure with a tape measure or a ruler" So we are going to remember how a measurement is read.

https://www.youtube.com/watch?v=WHqns716qiE&feature=youtu.be

  
Videos with simple explanations

           Carl Sagan - Cosmos – Eratosthenes           https://www.youtube.com/watch?v=G8cbIWMv0rI

           ERATOSTHENES    https://www.youtube.com/watch?v=wPR3XhIDP9w

            ERATÓSTENES Y LA MEDIDA DE LA TIERRA    https://www.youtube.com/watch?v=2tmiWjLSMcA

 
In this video let's see how the shadow moves. The shadow will begin to shorten its length until it reaches a pussycat and then it will begin to be longer. The shorter shadow is what we need.

https://www.youtube.com/watch?v=pnAlbwWBNSI
 
PROYECTO STICK (Original)

https://www.youtube.com/watch?v=QeQYYh6zW9I
 
Project Stick (Subtitled)

https://youtu.be/4VVx0RTLCEA

 Web pages to know the weather, (surely you know a better one)

https://weather.com
 
https://meteologix.com
 
https://www.windfinder.com/

https://www.windy.com/

 
Sign Up

http://form.stick.com.ar

 
Simulator

http://simu.stick.com.ar

 
Demonstration
Students may have difficulty understanding how the method presented here, with two schools along the same north-south line (the same meridian) working together, permits them to measure Earth’s radius on any day of the year. If you have a globe, mount two Straw pieces on the same meridian. Place the globe in the beam of an overhead projector. Ask a student to rotate the globe so the location of one straw is at local noon.
Ask what time it is at the other straw (local noon also).
How can they tell? (The shadows have mínimum length.) Have a student change the orientation of the globe axis and repeat.
A different way to visualize the geometry is to imagine the plane containing the center of Earth and points A and B. As Earth turns on its axis, this plane sweeps through all of space. When this plane is oriented so the sun lies within it, then the shadow of each stick lies within the plane as well, so it is local noon at the location of each stick.
 
Assessment
There are several ways to assess students’ performance in the Stick project.
• Students can choose one or more of the first three objectives and write or present the description that is specified in those objectives.
• Students can present a portfolio of student work, explanations, and drawings to show how they measured the radius of Earth.
• Students can prepare a written or oral presentation to a younger student on Eratosthenes’ measurement of the circumference of Earth.